Medical Testing

Introduction

One of the major applications of Bayes’ Theorem is in diagnosing heart disease. Bayes’ Theorem is used to calculate the probability of coronary artery disease based on clinical data and many noninvasive test results. For example, a past study of 154 patients referred for coronary arteriography were studied with stress electrocardiography (ST), stress thallium scintigraphy (Th), cine fluoroscopy (for coronary calcifications) (Ca), and coronary angiography. Pretest probabilities of coronary disease were determined based on age, sex, and type of chest pain (typical angina pectoris, atypical angina, nonanginal pain, and no pain). These pretest probabilities and pooled literature values for the conditional probabilities of test results based on disease state were used in Bayes' theorem to calculate posttest probabilities of heart disease.

Methodology

To gather the researchers’ data, they had the 154 patients undergo several tests, including but are not limited to exercise tests (treadmill exercise), injecting thallium-201 into their arm veins, nuclear imaging, and selective coronary arteriographic to obtain multiple projections of each vessel. The data obtained were analyzed by investigators unknown to the the observed clinical data and the results of the tests in order to eliminate any test-review bias that might occur. The investigator determined that a stenosis of greater than 50% of the intraluminal diameter of one of the four main coronary arteries was considered sufficient to classify a subject as having coronary artery disease.

In order to apply Bayes’ Theorem, the assumption that the three test variables (ST, Th, and Ca) and the clinical variables (age, sex, and type of chest pain) must be independent has to be met. The results of study did suggest that the assumption was met. The three test variables must be mutually independent. The test results also showed pairwise independence in patients with and without disease. Patients were divided into groups according to their pretest probabilities (high, intermediate, and low probability) of heart disease.

Results

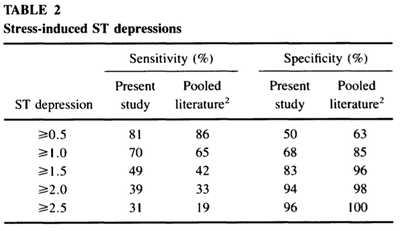
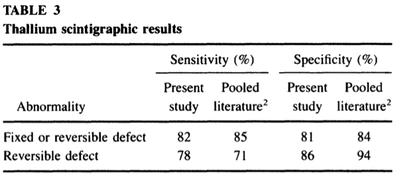
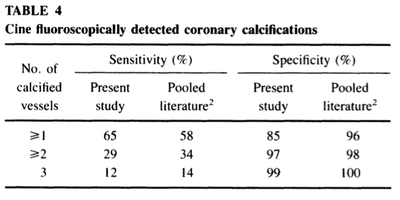
Tests sensitivities and specificities based on 154 patients were calculated based on the test results that were gathered and are presented in Tables 2-4. These values together with the pooled literature values from past research were used to calculate the posttest probabilities using Bayes’ Theorem.

Images retrieved from: Detrano, R., J. Yiannikas, E. E. Salcedo, G. Rincon, R. T. Go, G. Williams, and J. Leatherman. "Bayesian Probability Analysis: A Prospective Demonstration of Its Clinical Utility in Diagnosing Coronary Disease." Circulation 69.3 (1984): 541-47. Web.

Both the pretest and posttest probabilities were divided into probability subgroups: low (0 ≤ p < .2), intermediate (.2 ≤ p ≤ .8), and high (.8 < p ≤ 1.0). Each patient was assigned a pretest and a posttest subgroup. The number of patients for whom probability either advanced or retreated by at least one subgroup after testing was determined for patients with and those without heart disease.

Image retrieved from: Detrano, R., J. Yiannikas, E. E. Salcedo, G. Rincon, R. T. Go, G. Williams, and J. Leatherman. "Bayesian Probability Analysis: A Prospective Demonstration of Its Clinical Utility in Diagnosing Coronary Disease." Circulation 69.3 (1984): 541-47. Web.

Posttest probabilities calculated by Bayes’ Theorem correctly advanced 17 patients by at least 1 probability subgroup and moved back 7 patients.

For the 76 patients without disease, 34 were correctly moved into a lower probability subgroup while 10 were incorrectly moved up.

Mathematics Behind it All

General Solution to Introduction:

Examples

Since noninvasive test results only adds a bit more information to the clinicians’ assessment of patients to have coronary disease or not, there have been many attempts to combine tests results to better predict existence or nonexistence of coronary artery disease. With Bayes’ Theorem, the researcher could have a more refined probability for diagnostic assessments given the new information gained from the noninvasive test results. Posttest probabilities allowed the researchers to narrow down the number of patients that actually really need noninvasive test results. Therefore, this strategy would also lower the cost. However, the decision to send the patient for coronary arteriography should not be based solely on costs and the posttest probabilities calculated from Bayes’ Theorem but it should also take into consideration the researcher’s skill and experience, the safety and quality of the stress testing and the patient’s mental attitude about undergoing the test. Therefore, these posttest probabilities, however accurate they are, should never replace the researcher’s judgment in making his or her decision but they should be used a guide to interpreting the data. However, with certain limitations and inconsistencies in this study, posttest probabilities calculations made by using Bayes’ Theorem clearly more accurately predict coronary heart disease than did the pretest probabilities. The study found that Bayes’ Theorem does a fine job in separating patients who have heart disease from those that do not and therefore would greatly assist physicians in diagnosing the disease.

Video Example

Video retrieved from: "Bayes Theorem Example." YouTube. YouTube. Web. 16 Apr. 2015. <https://www.youtube.com/watch?v=Jht31ML2HxI>.

Drug Testing

Return to Home

Genetic Counseling